AB тест и механизм принятия решений

Механизм принятия решений на основе нулевой и альтернативной гипотезы (NHST¹) возник, как сочетание двух подходов Фишера и Неймана-Пирсона:

1. Проверка значимости Фишера: фокусируется на p-value, чтобы определить, соответствуют ли наблюдаемый результат нулевой гипотезе. Явной альтернативной гипотезы нет.

2. Проверка гипотез Неймана-Пирсона: включает как нулевую, так и альтернативную гипотезы и фокусируется на механизме принятии решений с компромиссом между ошибками и открытиями, определяя ошибки 1-го и 2-го рода.

Нулевая гипотеза предполагает отсутствие эффекта или различий между контрольной и тестовой группами, альтернативная гипотеза - наличие эффекта и различий. Цель тестирования - определить, насколько полученные данные противоречат нулевой гипотезе и соответственно подтверждают альтернативную гипотезу.

• Ошибка 1-го рода ($\alpha$) - отклонение нулевой гипотезы, когда она на самом деле верна. Уровень статистической значимости $\alpha$ определяет вероятность совершения ошибки 1-го рода.

• Ошибка 2-го рода ($\beta$) - принятие нулевой гипотезы, когда она на самом деле неверна. Мощность теста $1 - \beta$ определяет вероятность правильного отклонения нулевой гипотезы.

При этом существует математическая связь между альфой и бетой. А именно, альфа будет определять критическое значение, а критическое значение определяет бету. Это говорит о компромиссе между ошибкой и открытием.

$$MDE_{\hat\Delta} = (z_{1-\alpha/2} + z_{1-\beta}) \times SE_{\hat\Delta}$$

Если мы допустим бОльшее значение $\alpha$, у нас будет меньшее критическое значение, и для той же $\beta$ мы можем обнаружить меньший эффект в случае, если альтернативная гипотеза верна.

Если мы допустим бОльшее значение $\beta$, мы также можем обнаружить меньший эффект. То есть, если мы допустим больше ошибок (либо 1-го, либо 2-го рода), мы потенциально можем обнаружить меньший истинный эффект.

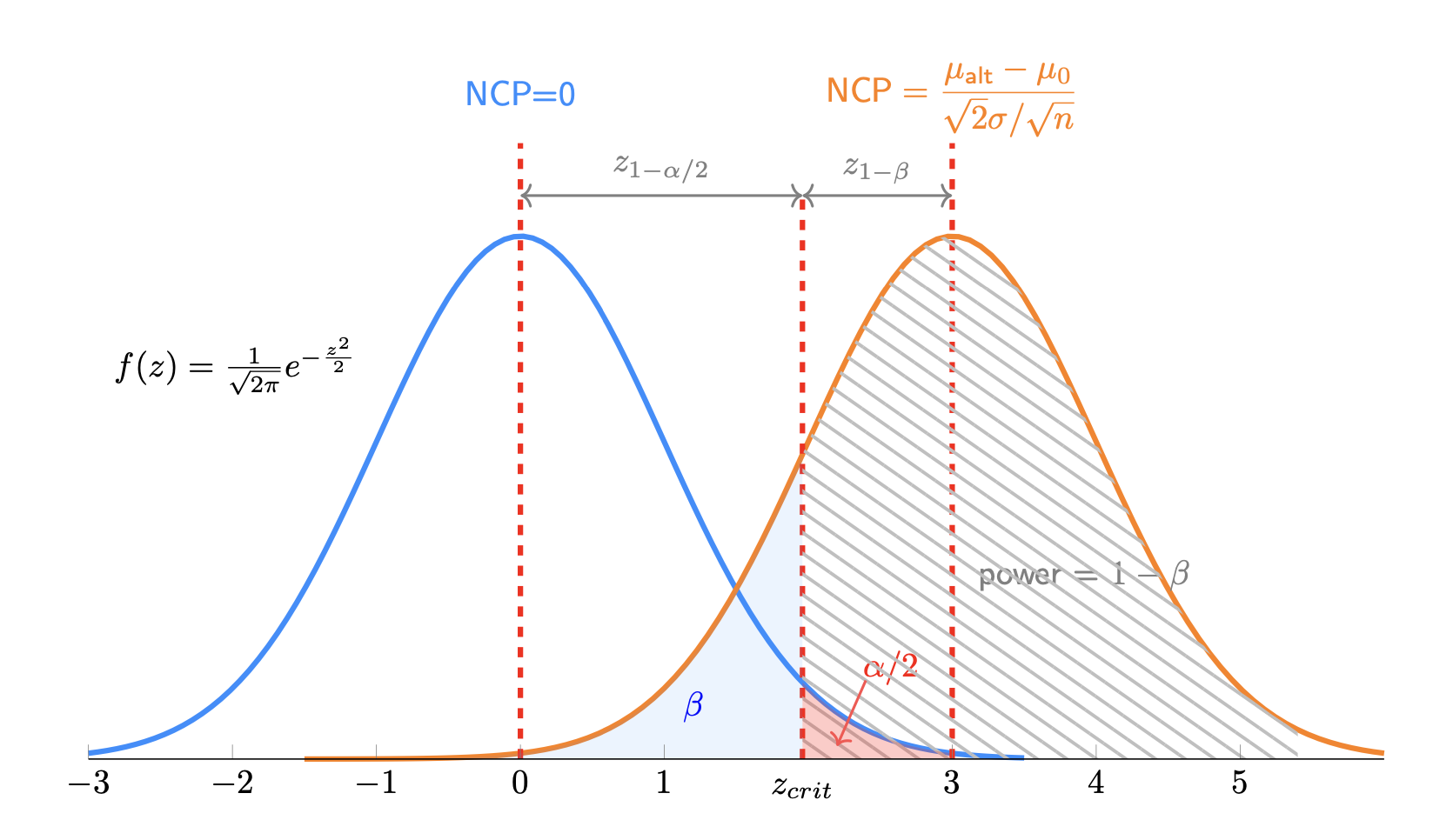
Рис 1. График z-распределений и параметр нецентральности NCP для нулевой и альтернативной гипотезы.

Мощность теста (Power) при этом будет определяться, исходя из следующей формулы:

$$z_{1-\beta} = \frac{MDE}{\sqrt{2 \cdot \frac{\sigma^2}{n}}} - z_{1-\alpha/2}$$

Зная $z_{1-\beta}$ для конкретного теста, можно легко найти мощность:

$$\begin{aligned} \text{Power} &= \Phi \left(z_{1-\beta}\right) \\ &= \Phi \left( \frac{\text{MDE}}{\sqrt{2 \cdot \frac{\sigma^2}{n}}} - z_{1-\alpha/2} \right) \\ &= \Phi \Bigl( \frac{\text{MDE}}{\sqrt{2 \cdot \frac{\sigma^2}{n}}} - \Phi^{-1}( 1-\dfrac{\alpha}{2}) \Bigr) \end{aligned}$$

где, $\Phi$ - это CDF стандартного нормального распределения, а $\Phi^{-1}$ - это обратная CDF.

Сравнение двух независимых выборок

Будем сравнивать две независимые выборки для непрерывной метрики. Пусть:

• $\mu_0 = 3000$ - среднее значение в контрольной группе
• $\mu_{\text{alt}} = 3030$ - среднее значение в тестовой группе, , т.е. эффект равен 30
• $\sigma = 700$ - стандартное отклонение метрики (в каждой группах)
• $n = 5000$ - размер выборки в каждой группе

Тогда стандартизированный эффект (Cohen's $d$) будет равен:

$$\begin{aligned} d &= \frac{\mu_{\text{alt}} - \mu_0}{\sigma} \\ &= \frac{3030 - 3000}{700} \\ &= 0.043 \end{aligned}$$

В случае равенства размеров выборок ($n_1 = n_2 = n$) и стандартных отклонений ($\sigma_1 = \sigma_2 = \sigma$) выборочный параметр нецентральности ($\lambda$) можно выразить так:

$$\begin{aligned} \lambda &= \frac{|\mu_1 - \mu_2|}{\sigma} \cdot \sqrt{\frac{n}{2}} \\ &= d \cdot \sqrt{\frac{n}{2}} \end{aligned}$$

В случае равенства размеров выборок и стандартных отклонений формула для стандартизированного эффекта (Cohen's $d$) упрощается до следующего вида:

$$d = \frac{|\mu_1 - \mu_2|}{\sigma}$$

Где:

• $\mu_1$ и $\mu_2$  - это средние значения генеральных совокупностей двух групп.
• $\sigma$  - стандартное отклонение, которое предположительно одинаково для обеих групп

Кохен предложил следующие критерии для интерпретации значения $d$. Эти значения являются эмпирическими ориентирами, используемыми для оценки значимости эффекта в контексте различных исследований.

• Маленький эффект: d = 0.2
• Средний эффект: d = 0.5
• Большой эффект: d = 0.8

Таким образом, для нашего примера, когда $d = 0.043$, это будет маленький эффект.

Визуализация графиков распределений

Предположим, что наша метрика распределена нормально. Визуализируем графики аналитических распределений нашей метрики (выручка на пользователя) для контрольной и тестовой групп:

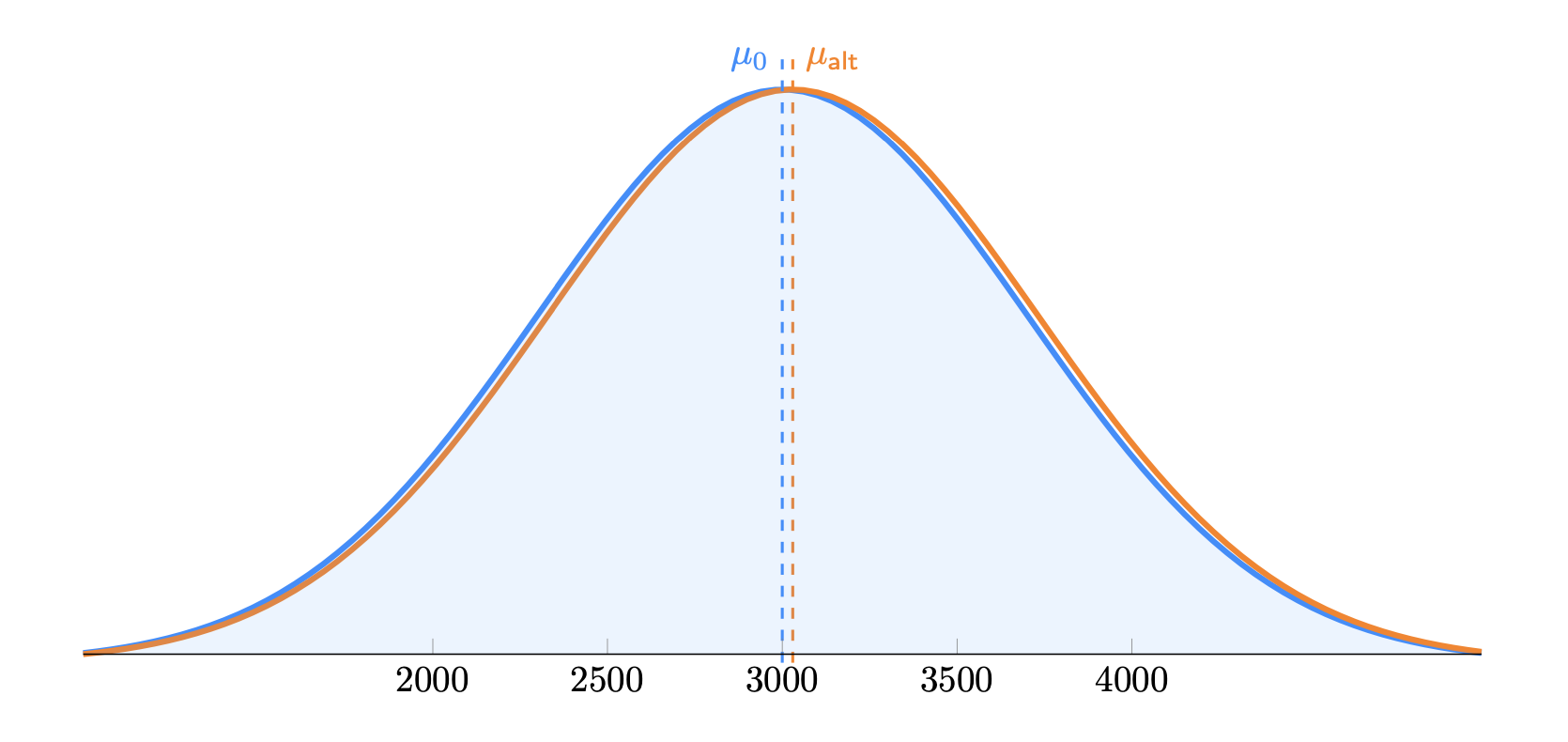
Рис 2. График аналитического распределения для контрольной и тестовой групп.

На практике метрика "выручка на пользователя" чаще распределена не нормально, а скорее логнормально, т.е. смещенная вправо, с длинным правым хвостом. При этом за счет логнормального распределения, среднее значение будет больше медианы. Дисперсия у логнормального распределения при прочих равных условиях будет больше, чем у нормального распределения. Это вносит дополнительную неопределенность в статистические тесты для проверки гипотез. Т.е. для статистически значимого результата, необходимо больше данных или более заметный эффект.

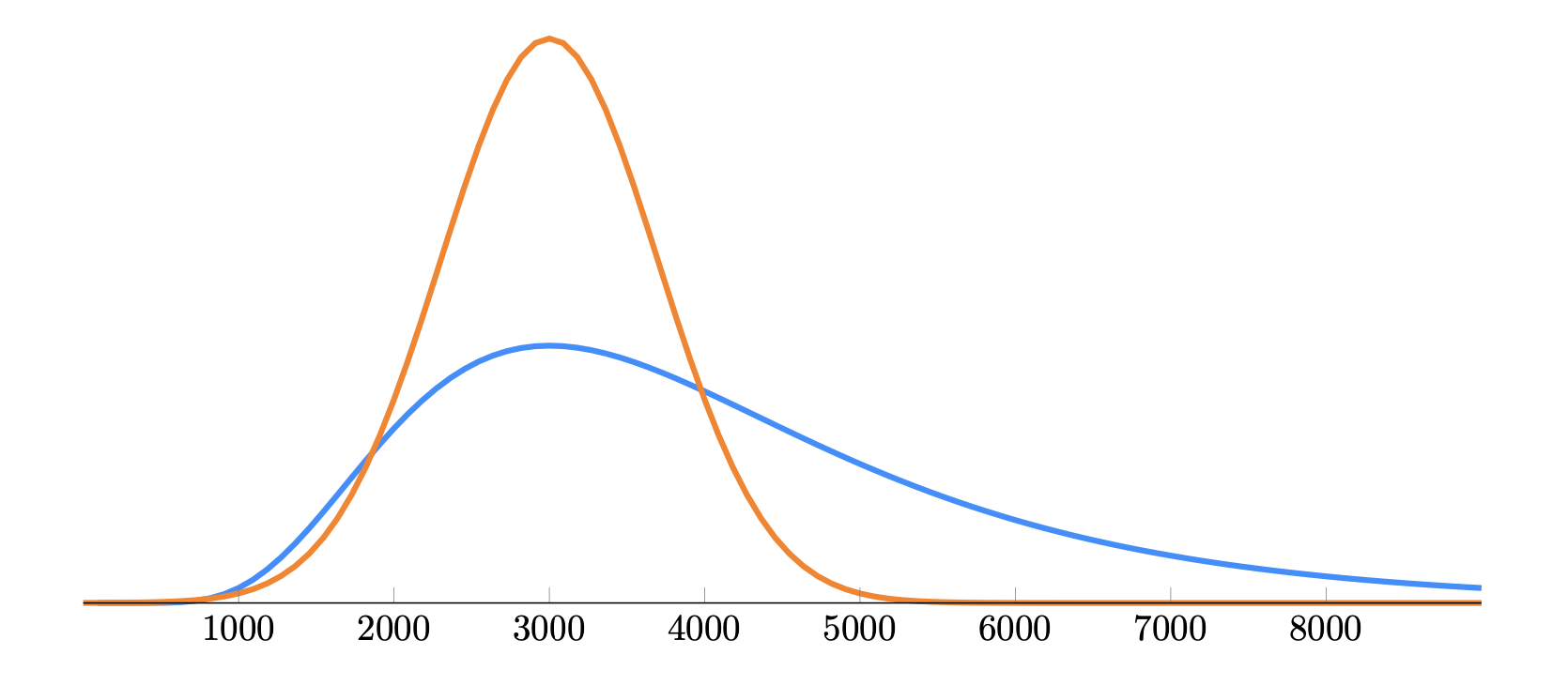
Рис 3. График сравнения нормального и логнормального распределения.

Принципы частотного фреймворка

Частотный подход (frequentist statistical framework) к вероятности основан на идее многократного повторения эксперимента. Пусть $n$ - количество испытаний, $n_A$ - количество благоприятных исходов, $p$ - вероятность благоприятного исхода. Тогда, частота благоприятного исхода $f = \frac{n_A}{n}$ будет стремиться к вероятности $p$ при $n \to \infty$.

$$\lim_{n \to \infty} f = p$$

В контексте нулевой и альтернативной гипотезы, частотный подход позволяет оценить вероятность получить наблюдаемые различия при условии, что нулевая гипотеза верна, и если эта вероятность меньше уровня значимости $\alpha$, то мы отклоняем нулевую гипотезу в пользу альтернативной.

Напомним, что для сравнения средних двух независимых выборок нулевая и альтернативная гипотезы выглядят следующим образом:

$$\begin{aligned} H_0 &: \mu_0 = \mu_{alt} \\ H_A &: \mu_0 \neq \mu_{alt} \end{aligned}$$

Визуализируем распределения метрики "выручка на пользователя" с длинным правым хвостом, как логнормальные распределения:

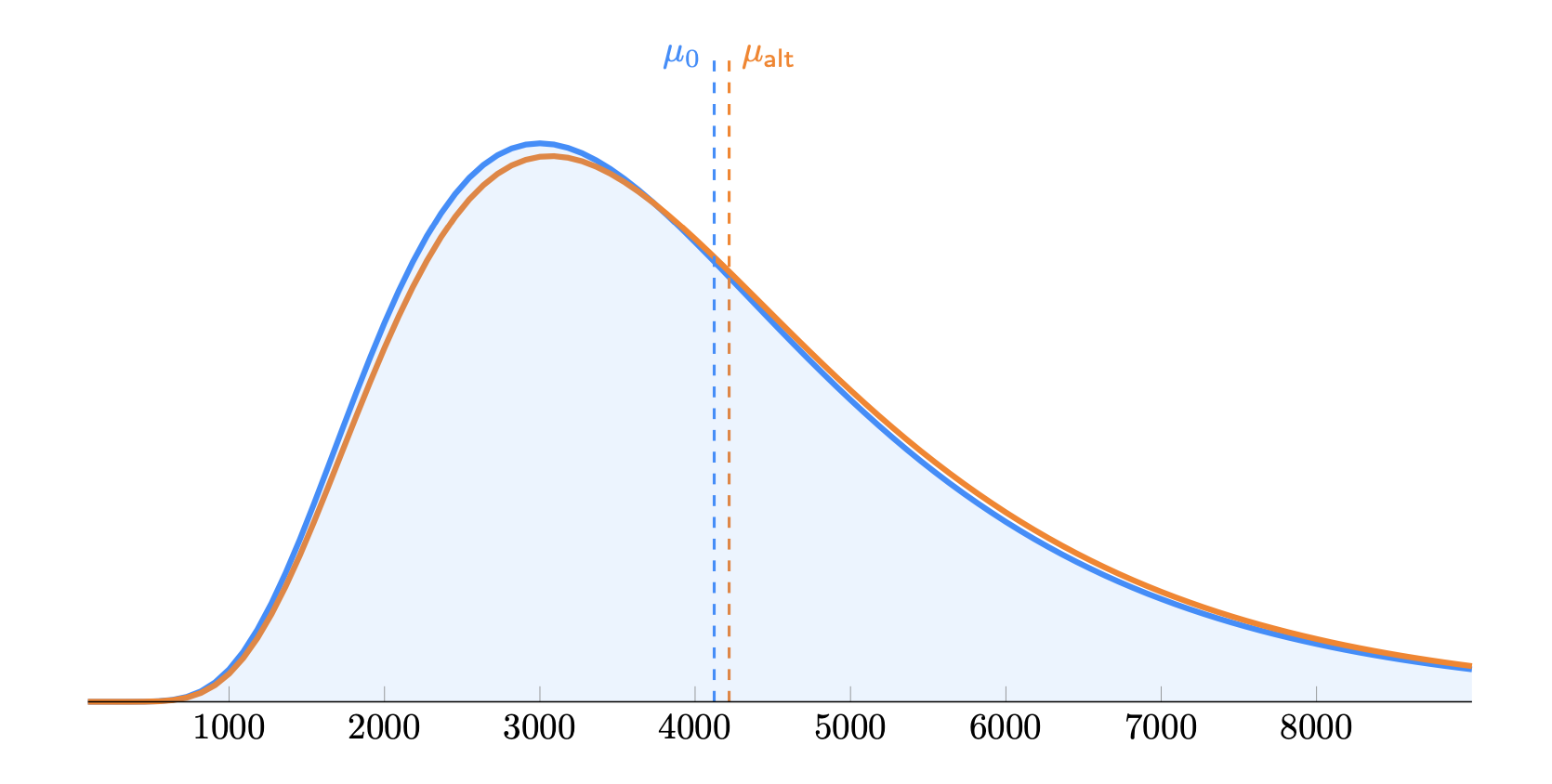
Рис 4. Графики распределения контрольной и тестовой группы при небольшом эффекте.

Как видно из вышеприведенного графика, при небольшом значении эффекта (d Кохена < 0.2) распределение для контрольной и тестовой групп выглядят практически идентично. Нам нужно некое "увеличительное стекло" для определения статистической значимости. Частотный фреймворк решает эту задачу с помощью сравнения выборочных средних, которые согласно ЦПТ будут распределены нормально.

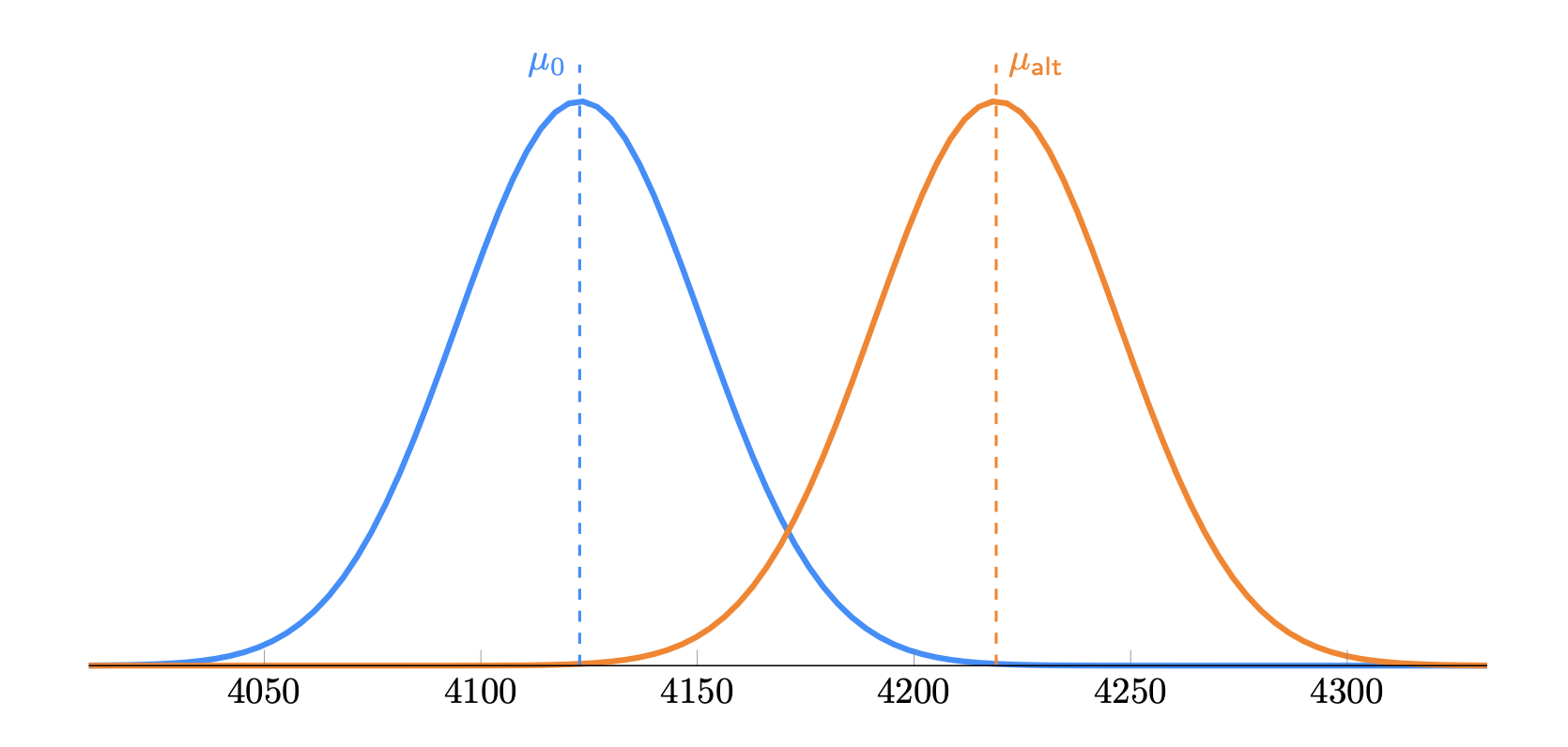
Рис 5. Графики распределения выборочных средних контрольной и тестовой группы.

Центральная предельная теорема (ЦПТ) утверждает, что по мере увеличения размера выборки $n$, распределение выборочных средних $\bar{x}$ стремится к нормальному распределению, даже если исходное распределение данных не является нормальным.

$$\bar{x} \stackrel{a}{\sim} N \left( \mu, \frac{\sigma^2}{n} \right)$$

Другими словами распределение выборочных средних будет иметь среднее значение приблизительно равное среднему значению генеральной совокупности $\mu$ (несмещенная оценка) и стандартное отклонение равное стандартной ошибке среднего $\sigma / \sqrt{n}$.

Эквивалентная формула имеет вид:

$$z = \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \stackrel{a}{\sim} N(0,1)$$

Статистический критерий

Вышеизложенное дает нам формулу для стандартизированной разницы средних двух независимых выборок:

$$\begin{aligned} z &= \frac{(\bar{x}_2 - \bar{x}_1) - (\mu_2 - \mu_1)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \\ &= \frac{\bar{x}_2 - \bar{x}_1}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \\ % &\stackrel{a}{\sim} N(0,1) \end{aligned}$$

Здесь $s$ - это стандартное отклонение выборки, а $n$ - размер выборки. Дисперсия для разницы средних значений двух независимых выборок соответственно равна:

$$\begin{aligned} \text{Var}(\bar{x}_2 - \bar{x}_1) &= \text{Var}(\bar{x}_2) + \text{Var}(\bar{x}_1) \\ &= \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \end{aligned}$$

Вышеприведенная формула для разницы средних позволяет сравнить два средних значения и определить, является ли разница между ними статистически значимой. Для двухстороннего теста разница будет статистически значимой, если подсчитанная $z$ (стандартизированная разница) превышает критическое значение $z_{1-\alpha/2}$ для уровня значимости $\alpha$ и соответственно p-value$< \alpha$, где p-value вычисляется по формуле:

$$\begin{aligned} \textit{p-value} &= 2 \cdot (1 - \Phi(|z|)) \end{aligned}$$

Этот критерий асимптотически соответствует тесту Студента/Уэлча (Student's/Welch's t-test) и используется для проверки гипотезы о равенстве средних значений двух независимых выборок при достаточно большом количестве наблюдений.