Дизайн A/B эксперимента
Опубликовано: Сентябрь 10, 2024
Дизайн эксперимента включает в себя:
- формулирование гипотезы,
- определение целей и задач эксперимента,
- выбор метрики успеха и других метрик и соответственно количества статистических тестов (каждая метрика - один тест),
- выбор метода разделения трафика,
- определение длительности эксперимента
- и другое
1. Фазы эксперимента
Каждый эксперимент можно разделить на три фазы, каждая фаза имеет свои цели и задачи:
-
Пред-экспериментальная фаза - дизайн эксперимента. На этой фазе определяются цели и задачи A/B теста, формулируются гипотезы, выбираются методы и инструменты для проведения эксперимента и оценки его результатов.
-
Экспериментальная фаза - проведение эксперимента, включает в себя запуск кода, сбор данных, валидацию данных, подготовку данных для анализа результатов. Эта фаза также может включать методы последовательного анализа данных, которые позволяют оценивать ход эксперимента с точки зрения целесообразности его продолжения.
-
Пост-экспериментальная фаза - анализ результатов эксперимента, включает в себя обработку данных, статистический анализ, интерпретацию результатов.
Разделение фаз позволяет более четко структурировать процесс проведения экспериментов. В отличие от проверки гипотез в оффлайн, где организация эксперимента сильно зависит от условий применения, в онлайн экспериментах с одной стороны можно контролировать многие факторы, что позволяет более точно оценивать результаты эксперимента, с другой вероятность технических ошибок возрастает, что приводит к необходимости дополнительных мер по обеспечению качества технической реализации.
Каждая фаза - это отдельная обширная глава в методологии со своими нюансами, подводными камнями и методами решения проблем. Ниже мы разберем каждую фазу более детально.
2. Формулирование гипотезы
Гипотеза - это предположение о том, как предполагаемое изменение повлияет на интересующую нас метрику. Гипотеза должна быть конкретной, измеримой и проверяемой.
Пример гипотезы для ecommerce вебсайта:
Гипотеза: Внедрение нового дизайна страницы корзины увеличит конверсию пользователей из корзины в покупку по сравнению с текущим дизайном. Ожидаемый эффект - увеличение конверсии на 1%.
Формулировка гипотезы в контексте NHST1:
Концепция нулевой и альтернативной гипотезы дает механизм принятия решения по результатам теста. Нулевая гипотеза предполагает отсутствие эффекта или различий между контрольной и тестовой группами, альтернативная гипотеза - наличие эффекта и различий. Цель тестирования - определить, насколько полученные данные противоречат нулевой гипотезе и соответственно подтверждают альтернативную гипотезу.
Для дизайна теста необходимо задать уровень статистической значимости, мощности теста, например: $\alpha = 0.05$ и Power = 0.8.
-
Нулевая гипотеза ($H_0$): Внедрение нового дизайна не повлияет на конверсию пользователей (разница в конверсии = 0). $$H_0: \text{CR}_A = \text{CR}_B$$
-
Альтернативная гипотеза ($H_1$): Внедрение нового дизайна повлияет на конверсию пользователей. Относительный MDE = 1%. $$H_1: \text{CR}_A \neq \text{CR}_B$$
Таким образом в данном примере CR - это наша метрика успеха, которую мы будем использовать для оценки эффективности изменений, и фактически мы будем проводить двусторонний статистический тест для двух независимых выборок с выбранными значениями $\alpha$ и $\beta$.
| Гипотеза | Тип ошибки | Определение | Почему это важно | Значение | Критическое значение |
|---|---|---|---|---|---|
| $H_0$ | Ошибка 1‑го рода | Отклонение нулевой гипотезы, когда она верна | Позволяет избежать ложных выводов | $\alpha = 0.05$ | $z_{1-\alpha/2} = 1.96$ |
| $H_1$ | Ошибка 2‑го рода | Принятие нулевой гипотезы, когда она неверна | Позволяет избежать пропуска реальных эффектов. Определяет мощность теста: Power = $1-\beta$ | $\beta = 0.2$ | $z_{1-\beta} = 0.84$ |
Иллюстрация и описание тестируемого дизайна или фичи:
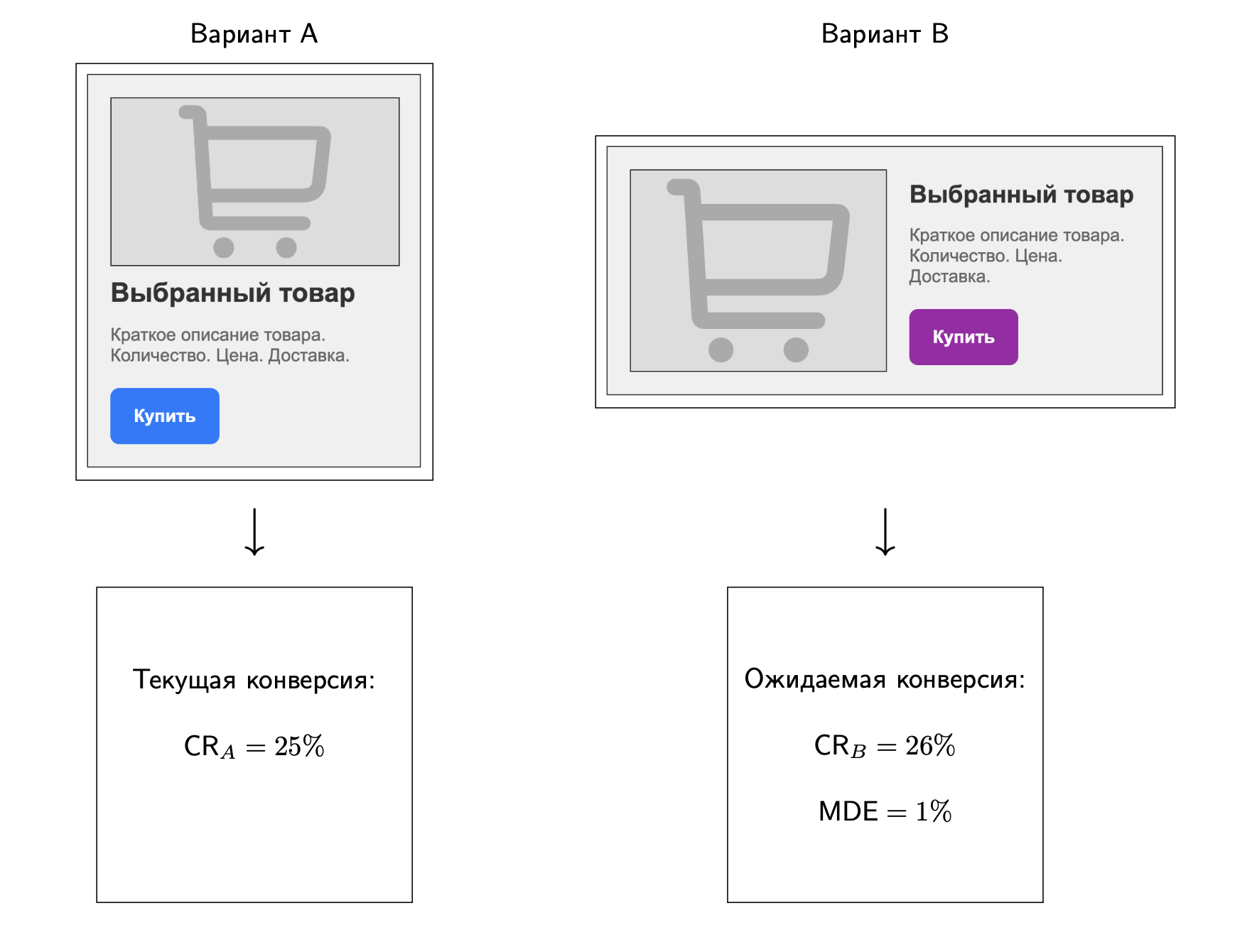
Описание дизайна или фичи должно пояснять суть тестируемого изменения, обоснование MDE (minimum detectable effect), MEI (minimum effect of interest) и выбора метрики успеха.
3. Выбор метрики успеха
Метрика успеха (success metric) - это показатель, который позволяет оценить эффективность изменений, внесенных в продукт. Метрика должна быть чувствительной к изменениям, измеримой, надежной и интерпретируемой.
Пример метрики успеха для ecommerce вебсайта:
Метрика успеха: Конверсия пользователей из корзины в покупку (CR). Метод расчета - поюзерный:
$$\text{Конверсия (CR)} = \frac{\text{Количество пользователей, совершивших покупку}}{\text{Количество пользователей, перешедших в корзину}}$$
4. Дополнительные метрики
В зависимости от целей эксперимента и особенностей продукта, могут быть выбраны и другие метрики, такие как: средний чек, количество покупок, количество просмотров страницы, время на странице, количество кликов и т.д.
| Метрика | Тип метрики | Определение | Почему это важно | Изменение | Статзначимость | MDE |
|---|---|---|---|---|---|---|
| Процент бросания корзины | информативная блокирующая | Процент пользователей, не завершающих покупку | Выявляет вероятность завершения покупок. Не должна снижаться. | = | = | = |
| Средний чек (AOV) | информативная блокирующая | Средняя стоимость заказа | Отражает финансовую эффективность. Не должна снижаться. | = | = | = |
| Время от корзины до покупки | информативная | Среднее время от посещения корзины до покупки | Отражает удобство пользования корзиной | = | = | = |
| Доход на покупателя (ARPPU) | информативная блокирующая | Средняя выручка на покупателя | Отражает финансовую эффективность. Не должна снижаться. | = | = | = |
Колонки "Изменение", "Статзначимость" и "MDE" заполняются после проведения эксперимента. В колонке "Изменение" можно указать значения метрики для контрольной и тестовой группы, абсолютное и относительное изменение.
Важно отметить, что в данном случае MDE - это расчет минимально замеримого эффекта на пост экспериментальном этапе. В данном случае MDE позволяет оценить чувствительность соответствующего теста при выбранных значениях $\alpha$ и $\beta$ и фактическом размере выборки с фактической дисперсией в контрольной и тестовой группах:
$$\begin{aligned} MDE_{post\_exp} = (z_{1-\alpha/2} + z_{1-\beta}) \cdot \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \end{aligned}$$
где:
- $n_1 \approx n_2$ - размер выборок в контрольной и тестовой группах,
- $s_1^2, s_2^2$ - дисперсии в контрольной и тестовой группах.
5. Определение длительности эксперимента
Длительность эксперимента зависит от нескольких факторов, таких как размер ожидаемого эффекта, длительность цикла продаж, факторов сезонности и т.д. Длительность должна быть достаточной для того, чтобы получить статистически значимые результаты. Математически длительность эксперимента привязана к определению минимального размера выборки (n), который необходим для обнаружения заданного эффекта с заданной мощностью и уровнем значимости, либо к определению минимального размера эффекта (MDE), который можно обнаружить с заданной мощностью и уровнем значимости.
Разница в двух подходах заключается в том в том, можем ли мы достаточно точно оценить ожидаемый эффект или нет. Если мы можем оценить ожидаемый эффект, то мы можем определить размер выборки, который необходим для обнаружения этого эффекта. Если мы не можем оценить ожидаемый эффект, то мы можем определить минимальный размер эффекта, который мы можем обнаружить с заданной мощностью и уровнем значимости.
В случае попользовательской рандомизации и, предполагая равные пропорции контрольной и тестовой группы, формула для расчета размера выборки для непрерывной метрики (например, выручка) имеет вид:
$$n = 2 \cdot \frac{(z_{1-\alpha/2} + z_{1-\beta})^2 \cdot \sigma^2}{\delta^2}$$
где:
- $n$ - размер выборки в каждой группе,
- $z_{1-\alpha/2}$ и $z_{1-\beta}$ - квантили стандартного нормального распределения для выбранной значимости и мощности соответственно,
- $\sigma$ - стандартное отклонение метрики,
- $\delta$ - минимальное практически значимое изменение метрики в абсолютных величинах, которое мы хотим иметь возможность обнаружить.
Такой подход называется фиксированный горизонт времени, поскольку, зная минимальное количество наблюдений, можно рассчитать длительность эксперимента, исходя из предполагаемого количества пользователей на данном временном интервале, которые попадут в эксперимент.
Для расчета MDE на этапе дизайна эксперимента можно использовать следующую формулу:
$$MDE_{pre\_exp} = (z_{1-\alpha/2} + z_{1-\beta}) \cdot \sqrt{2 \cdot \frac{\sigma^2}{n}}$$
где:
- $n$ - размер выборки одной группы,
- $\sigma$ - стандартное отклонение метрики (контрольной группы). Поскольку мы проводим тест для двух независимых выборок, то на пред-экспериментальном этапе мы как бы предполагаем, что стандартное отклонение в тестовой группе будет таким же, как и в контрольной группе.
Здесь MDE - это абсолютная величина. Предполагаются равные размеры контрольной и тестовой группы.
Схема двух подходов к дизайну эксперимента:
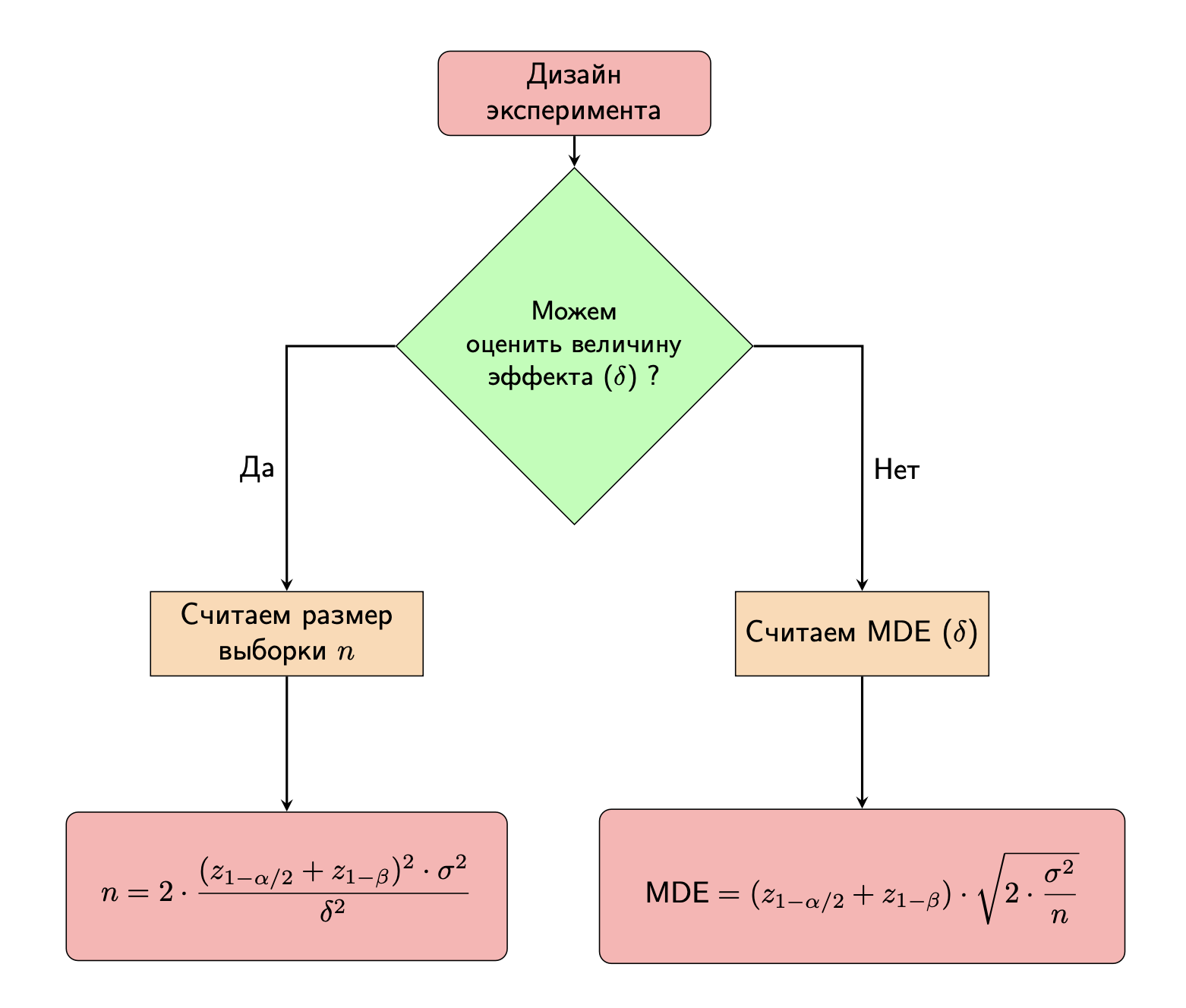
Для пропорций, для метрики конверсии (CR) в частности, формула для расчета размера выборки имеет вид:
$$n = 2 \cdot \frac{(z_{1-\alpha/2} + z_{1-\beta})^2 \cdot \bar p \cdot (1-\bar p)}{\delta^2}$$
где:
- $n$ - размер выборки в каждой группе,
- $\bar p = (p_0+p_1)/2$,
- $\delta = (p_1-p_0)$.
Обратите внимание, что разница между двумя формулами заключается только в том, как вычисляется стандартное отклонение. Обе формулы - это стандартный расчет размера выборки.
Если мы хотим для расчета использовать относительную разницу $\delta_{rel} = \delta / p_0$, и, например, посчитать $n$ для $\delta_{rel} = 0.03 \;(3\%)$, то формула примет вид:
$$n = 2 \cdot \frac{(z_{1-\alpha/2} + z_{1-\beta})^2 \cdot \bar p \cdot (1-\bar p)}{(p_0 \cdot \delta_{rel})^2}$$
Формула для расчета MDE на этапе дизайна эксперимента для пропорций имеет вид:
$$MDE_{pre\_exp} \approx (z_{1-\alpha/2} + z_{1-\beta}) \cdot \sqrt{2 \cdot \frac{p_0 \cdot (1-p_0)}{n}}$$
Здесь MDE - это абсолютная величина. Предполагаются равные размеры контрольной и тестовой группы.
В данной формуле мы поставили знак приблизительного равенства, поскольку мы предполагаем, что дисперсия в контрольной и тестовой группах одинакова, но для пропорций в случае наличия эффекта это предположение заведомо не выполняется.
6. Вывод
Правильное проектирование эксперимента является ключевым моментом для надежного A/B тестирования. Основные шаги включают:
- формулирование гипотезы,
- выбор метрики успеха,
- определение длительности эксперимента,
- расчет размера выборки или MDE.
Python и соответствующие статистические библиотеки можно использовать для эффективного расчета параметров и результатов эксперимента.
-
NHST - Null Hypothesis Significance Testing (Проверка статзначимости нулевой гипотезы) ↩